快速排序

我们先来模拟一下快速排序的流程

  1. 先寻找一个基值
  2. 将大于这个值的数放在它后面,小于的放在前面
  3. 递归调用前后两个已经分好的区间重新快排

GIF如下

img

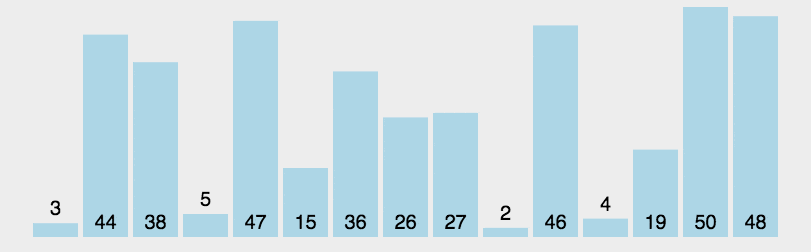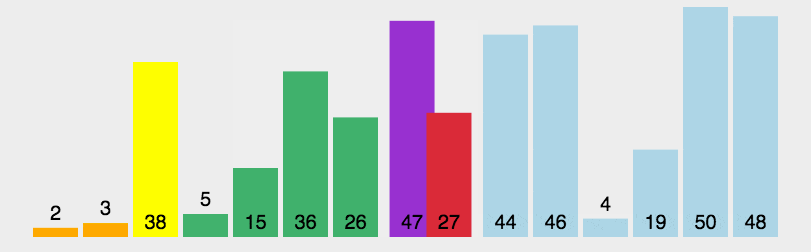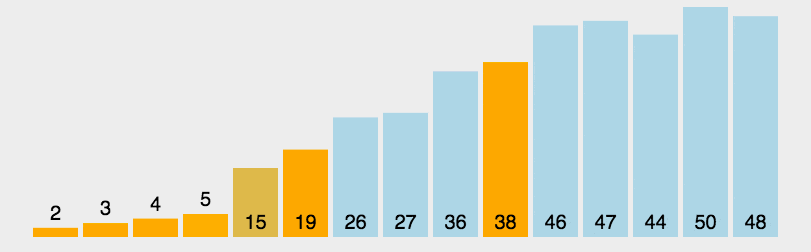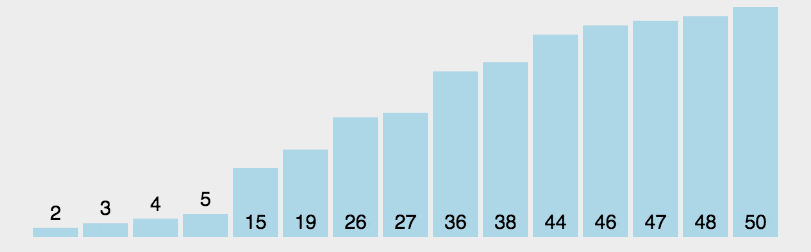
实现过程 (y总方法)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
// 闭区间使用右指针作为分界点
void quick_sort(int q[], int l, int r)
{
    if (l >= r) return;

    int i = l - 1, j = r + 1;
  	int x = q[l + r >> 1]; // 有可能取到左边界
    while (i < j)
    {
        do i ++ ; while (q[i] < x);
        do j -- ; while (q[j] > x);
        if (i < j) swap(q[i], q[j]);
    }

    quick_sort(q, l, j); // 以j为分界点递归,区间为[ l , j ]
    quick_sort(q, j + 1, r); // 以j为分界点递归,区间为[ j + 1 , r ]
}

// 左闭右开区间 [ l , r ) 使用右指针作为分界点
void quick_sort(int a[], int l, int r)
{
    if(r - l <= 1) return;
    
    int q = l - 1, p = r;
    int x = a[l + r >> 1]; // 有可能取到右边界
    
    while(q < p){
        do q++; while(a[q] < x);
        do p--; while(a[p] > x);
        if(q < p) swap(a[q],a[p]);
    }
    
    quick_sort(a,l,q); // 以q为分界点递归,区间为[ l , q )
    quick_sort(a,q,r); // 以q为分界点递归,区间为[ q , r )
}

1.我们先要确定怎么取一个基值作为对比

  • a[l]
  • a[l+r >> 1]
  • a[r]
  • a中的随机数

2.如何将小于和大于x的数分别位于两边 ( 交换位置 )

比如说我们可以定义两个数组,分别比较每一个数和x的关系,如果大于则放入一个大于数组,小于放入一个小于数组.

1
2
3
int greater[],less[];
if(a[i] > x) x->greater
else x->less

使用数组会占用额外的空间,我们可以直接使用双指针,在原数组的基础上修改数据.

定义一个左指针q和一个右指针p 分别从两边向中间迭代,如果遇到a[q] > x或者a[p] < x就停止迭代并交换两指针数据

1
2
3
4
5
while(q < p){
  while(a[q] < x) q++;
  while(a[p] > x) p--;
  if(q < p) swap(a[q],a[p]);
}

这里有几个坑需要注意

为什么是a[q] < x 而不是<=

我们要考虑到一种情况,比如说 基值选到最大值 的话,数组内所有元素都是小于等于基值的,指针可能会发生越界问题,或者死循环.

例如这组数据

1
9 5 7 2 4 8 3 1

如果基值一开始取到了9,那么左指针会不断移动,直到最后一个数据之后.或者再递归还是调用的原数组,会死循环下去

为什么交换时要判断q < p

通过每一次指针的移动,最后一次while循环的时候q和p有可能会移动到对方的遍历过的区间,此时再交换已经失去了原本的含义

比如

1
1 4 3 2 5 6 9 7

执行最后一次while后a[p] = 2 , a[q] = 5此时交换还有意义吗?

这时候指针不需要交换且执行完后会直接停止.

关于while循环的问题

上述代码其实是一段错误的代码

正常思维一拍脑袋想到的其实就是这样,为什么是错误的代码?

我们模拟一下指针的变化,如果出现相同数据的话,此处又会陷入一个死循环

例如这种情况

1
5 2 5 4 2 5 3 8

如果基值选择的是5的话

最后执行到a[q] = 5, a[p] = 5的时候, p q指针都会停止移动,并且不断重复swap的操作,就会陷入一个死循环.

要避免这种操作只需要让两个指针先移动再判断

1
2
3
4
5
6
7
8
9
10
11
12
while(q < p){
    while(a[++q] < x) ;
    while(a[--p] > x) ;
    if(q < p) swap(a[q],a[p]);
}
  // 或者
while(q < p){
    do q++; while(a[q] < x);
    do p--; while(a[p] > x);
    if(q < p) swap(a[q],a[p]);
}
边界问题

首先要搞清楚取中间值边界问题

假设一个数组a[10]

1
2
3
l = 0, r = 10
l + r >> 1 //下标会取到5
l + r - 1 >> 1 //下标会取到4

也就是说 如果用数组内的大小来表示r的话, 除于二的值会取到中间靠右的位置

反之会靠左

极限情况是只有两个数的时候,会取到左边那个还是右边那个这种情况要考虑清楚

解决了这个问题我们来看下一个问题

1
2
quick_sort(a, l, ?);
quick_sort(a, ?, r);

我们要考虑?中需要填写什么参数

最后一个问题也是最终要的一个边界问题如这种情况

1
1 8 7 3 5 4 2 9

如果基值选择a[l]

那么就会有一个问题, 指针停下来的时候q = 0, p = 0

下一次调用左区间为 [ l ,0 ) ,直接返回,而右区间[ 0 , r]又是原来相同的区间,

1
2
quick_sort(a, l, p); 
quick_sort(a, p, r); // 这层递归还是在原区间执行相同操作

所以 右指针移动到最左边的情况时 下一次递归使用右指针作为边界判断的条件时, 要+1 

1
2
quick_sort(a, l, p + 1); 
quick_sort(a, p + 1, r); // 这层递归还是在原区间执行相同操作

如果使用左指针划分区间的话 在递归时不需要-1

因为我们使用开区间进行递归,所以包含左边界但是不包含有边界.

极限情况下右边界会自动剔除

比如指针取到最后一个数下标为7

1
2
quick_sort(a, l, q);  // 区间为 [ l , q )
quick_sort(a, q, r);  // 区间为 [ q , r )

第一个区间是默认不包含最后一个数的,所以不需要-1的操作