A-莲子的软件工程学

题目背景

在宇宙射线的轰击下，莲子电脑里的一些她自己预定义的函数被损坏了。

对于一名理科生来说，各种软件在学习和研究中是非常重要的。为了尽快恢复她电脑上的软件的正常使用，她需要尽快地重新编写这么一些函数。

题目描述

具体而言，给定两个整数 $a,b$，保证 $b\neq 0$。莲子要实现这样一个函数 $\operatorname{fun}(a,b)$ 来将 $b$ 的符号转移到 $a$ 上。

具体而言，$\operatorname{fun}(a,b)=\operatorname{sgn}(b)\times |a|$。其中，$\operatorname{sgn}(b)=\begin{cases}1&b>0\-1&b<0\end{cases}$

换而言之：

如果 $b$ 是正数，那么 $\operatorname{fun}(a,b)=+|a|=|a|$；
如果 $b$ 是负数，那么 $\operatorname{fun}(a,b)=-|a|$。

如果使用一个三维坐标系描述 $\operatorname{fun}(a,b)$，则应当如下图所示：

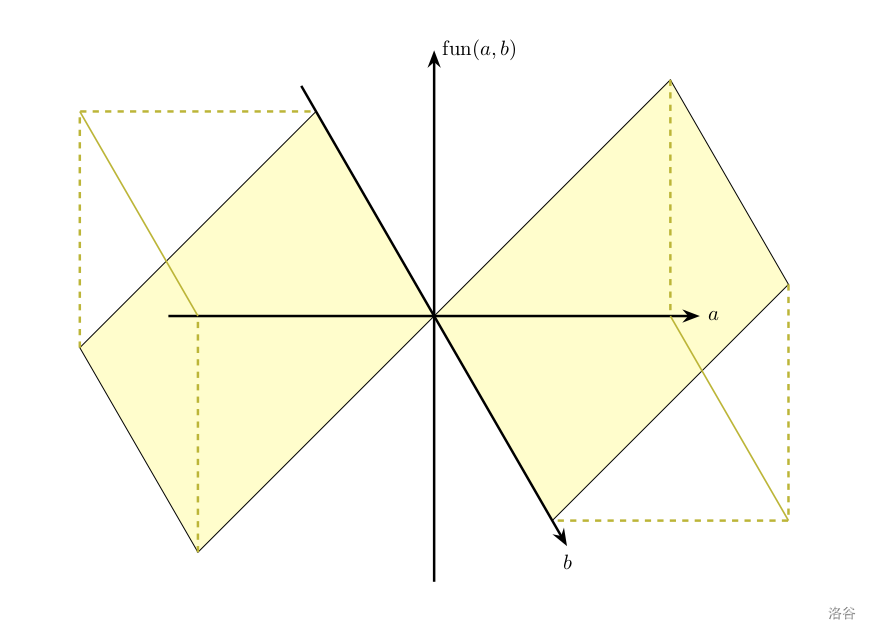
你只需输出 $\operatorname{fun}(a,b)$ 的值。

输入格式

共一行两个整数 $a,b$。

输出格式

共一行一个整数 $\operatorname{fun}(a,b)$ 的值。

样例 #1

样例输入 #1

-1 2

样例输出 #1

样例 #2

样例输入 #2

0 -4

样例输出 #2

样例 #3

样例输入 #3

1	-12345 -54321

样例输出 #3

-12345

提示

对于全部数据，保证 $a,b$ 在 $32$ 位有符号整型范围内，并且 $b \neq 0$。

#include <cstdlib>
#include<iostream>
using namespace std;

int main(){
    int a,b;
    cin >> a >> b;
    if(b < 0) a = -1 * abs(a);
    else a = abs(a);
    cout << a;
	return 0;
}

B-莲子的机械动力学

题目背景

【题目背景和题目描述的两个题面是完全等价的，您可以选择阅读其中一部分。】

专攻超统一物理学的莲子，对机械结构的运动颇有了解。如下图所示，是一个三进制加法计算器的（超简化）示意图。

一个四位的三进制整数，从低到高位，标为 $x_1,x_2,x_3,x_4$。换言之，这个数可以写成 $\overline{x_4x_3x_2x_1}_{(3)}$。把它放在这四个齿轮里，对应箭头指向的数字就是现在这位的数值。

在这种机械式计算机里，我们通过齿轮的啮合来实现数位间的连接。通过不同齿轮半径的比例来确定进制。图中所有浅灰色的小齿轮的半径，比上使用皮带相接的较大齿轮的半径，都是 $1:3$。那么小齿轮每转动一圈，大齿轮就转动 $\dfrac{1}{3}$ 圈，也就是刚好一个数码的角度。

于是，我们通过控制齿轮的半径实现了 $3$ 进制的进位。

如果需要实现三进制加法，则只需要在对应数位拨动对应的数码长度即可。

如下是个例子，实现 $\overline{1021}{(3)}+\overline{0021}{(3)}=\overline{1112}_{(3)}$

初始时齿轮的状态如上。

把第一个齿轮拨动一个单位长度，变为如上图所示。

把第二个齿轮拨动两个单位长度，变为如上图所示。读数，得到结果 $\overline{1112}_{(3)}$。

现在莲子设计了如下图所示的机械结构。对于从左往右数的第 $i$ 枚齿轮，它上面的浅色小齿轮与第 $i+1$ 枚齿轮上的深色小齿轮的半径之比为 $1:(i+2)$。也就是说，第 $i$ 枚齿轮每转动 $1$ 圈，第 $i+1$ 枚齿轮转过的角度恰好为它上面的一个数码。

莲子想要知道，在这样的特别的进制表示下，给定 $a,b$，那么计算出的 $a+b$ 的结果是多少。

题目描述

题目背景的问题可以转化为如下描述：

给定两个长度分别为 $n,m$ 的整数 $a,b$，计算它们的和。

但是要注意的是，这里的 $a,b$ 采用了某种特殊的进制表示法。最终的结果也会采用该种表示法。具体而言，从低位往高位数起，第 $i$ 位采用的是 $i+1$ 进制。换言之，相较于十进制下每一位的「逢 $10$ 进 $1$」，该种进制下第 $i$ 位是「逢 $i+1$ 进 $1$」。

下图所示，左边是十进制的竖式加法；右边是这种特殊进制的竖式加法。图中的红色加号表示上一位发生了进位。

输入格式

第一行有两个整数 $n,m$，分别表示 $a$ 和 $b$ 的位数。
第二行有 $n$ 个整数，中间用空格隔开，从高到低位描述 $a$ 的每个数码。
第三行有 $m$ 个整数，中间用空格隔开，从高到低位描述 $b$ 的每个数码。

输出格式

输出有若干个整数，从高到低位输出 $a+b$ 在这种特殊表示法下的结果。

样例 #1

样例输入 #1

1
2
3

5 4
3 3 2 1 1
3 2 2 1

样例输出 #1

4 2 1 1 0

样例 #2

样例输入 #2

1
2
3

10 1
10 9 8 7 6 5 4 3 2 1
0

样例输出 #2

1	10 9 8 7 6 5 4 3 2 1

提示

对于全部数据，保证 $1\le n,m\le 2\times 10^5$，从低位往高位数起有 $a_i\in[0,i]$，$b_i\in[0,i]$。请使用 Java 或 Python 语言作答的选手注意输入输出时的效率。

我的答案

#include <algorithm>
#include <cstdlib>
#include<iostream>
#include <vector>
using namespace std;


int main(){
    long n,m;
    vector<long long> a,b;
    cin >> n >> m;
    a.resize(n);
    b.resize(m);
    for(int i = 0; i < n ;i++) cin >> a[i];
    for(int i = 0; i < m ;i++) cin >> b[i];
    reverse(a.begin(),a.end());
    reverse(b.begin(),b.end());
    m = max(n,m);
    a.resize(m , 0);
    b.resize(m , 0);
    int it = 2;
    int add = 0;
    vector<long long> ans;
    for(int i = 0;i < m;i ++){
        int sum = a[i] + b[i] + add;
        add = sum / it;
        sum %= it; 
        ans.push_back(sum);
		it++;
    }
    for (int i = ans.size()-1 ; i>=0;i--) {
        cout << ans[i] << ' ';
    }
	return 0;
}

D-莲子的物理热力学

题目背景

莲子正在研究分子的运动。

每个分子都有一个速度，约定正方向为正，负方向为负。分子的数量极多，速度又并不一致，看上去杂乱无章。于是莲子希望调整部分分子的速度，使得最终分子们看上去整齐。

题目描述

莲子给定了 $n$ 个整数 $a_1,a_2,\cdots a_n$，描述每个分子。现在她可以进行至多 $m$ 次操作（也可以一次也不进行），每次操作可以执行以下两条之一：

选择 $i$，满足 $a_i=\min_j{a_j}$，然后将 $a_i$ 变为 $\max_j{a_j}$。
选择 $i$，满足 $a_i=\max_j{a_j}$，然后将 $a_i$ 变为 $\min_j{a_j}$。

现在莲子希望需要最小化最终序列的极差（最大值减去最小值的差）。请求出最小的极差。

例如，对于序列 $a={5,1,4}$，可以进行如下几次操作：

选择 $i=1$，满足 $a_1=5$ 是当前的最大值 $5$，可以将 $a_1$ 修改成当前的最小值 $1$，此时序列变成 ${1,1,4}$；
再选 $i=2$，满足 $a_2=1$ 是当前的最小值 $1$，可以将 $a_2$ 修改成当前的最大值 $4$，此时序列变成 ${1,4,4}$。

这两次操作后得到的序列为 ${1,4,4}$。最大值减去最小值的差为 $|4-1|=3$。

当然，这种操作方式得到的极差并非最小。最优策略是，先将最大值 $a_1=5$ 变成目前的最小值 $1$，再把此时的最大值 $a_3=4$ 变成目前的最小值 $1$。此时序列为 ${1,1,1}$，得到的极差 $|1-1|=0$ 是所有策略中最小的。

输入格式

第一行有两个正整数 $n,m$，分别表示序列的长度和你最多可以进行的操作次数。
第二行有 $n$ 个整数 $a$，描述给定的序列。

输出格式

输出共一行一个整数，表示最优策略下能得到的最小极差。

样例 #1

样例输入 #1

1
2

3 2
5 1 4

样例输出 #1

样例 #2

样例输入 #2

1 2	8 0 1 2 3 4 5 6 7 8

样例输出 #2

样例 #3

样例输入 #3

1 2	8 3 1 5 5 5 6 6 9 10

样例输出 #3

提示

样例解释

样例 $1$：${5,1,4}\to{1,1,4}\to{1,1,1}$，极差为 $0$。
样例 $2$：${1,2,3,4,5,6,7,8}$，什么也做不了，极差为 $7$。
样例 $3$：${1,5,5,5,6,6,9,10}\to{10,5,5,5,6,6,9,10}\to{5,5,5,5,6,6,9,10}\to{5,5,5,5,6,6,9,5}$，极差为 $4$。

数据范围及约定

对于全部数据，保证 $1\le n \le 10^5$，$0\le m\le10^9$，$|a_i|\le 10^9$。

E-梅莉的市场经济学

题目背景

如果遇到提交失败，请多次刷新，多次提交，会有成功几率

梅莉这个学期选修了经济学。但是主修心理学的她实在不擅长经济领域的分析，为此她时常抱怨自己学不会，想退课。

但是如果现在退掉的话这学期的学分就不够啦，因此她根据“梦中”的经历，“胡诌”了一个简单到不现实的市场模型，并依据这个模型编起了 essay。为了方便地编出图表，她需要写一个程序来查询每个时刻的市场贸易差。

题目描述

市场每一天的贸易差可以视为一个有周期性规律的数列 $a$：$\color{red}[0],\color{blue}[0,\allowbreak 1,\allowbreak 0,\allowbreak -1,\allowbreak 0],\color{red}[0,\allowbreak 1,\allowbreak 2,\allowbreak 1,\allowbreak 0,\allowbreak -1,\allowbreak -2,\allowbreak -1,\allowbreak 0],\allowbreak \color{blue}[0,\allowbreak 1,\allowbreak 2,\allowbreak 3,\allowbreak 2,\allowbreak 1,\allowbreak 0,\allowbreak -1,\allowbreak -2,\allowbreak -3,\allowbreak -2,\allowbreak -1,\allowbreak 0]\dots$ 具体而言，$a$ 可以被分为无穷段，第 $i$ 段的内容为 ${0,\allowbreak 1,\allowbreak \cdots,\allowbreak i,\allowbreak i-1,\allowbreak \cdots,0,\allowbreak -1,\allowbreak \cdots,\allowbreak -i,\allowbreak -i+1,\allowbreak \cdots 0}$。如下图所示，是将 $a$ 数列内的前一些点绘制在坐标轴上的情况：

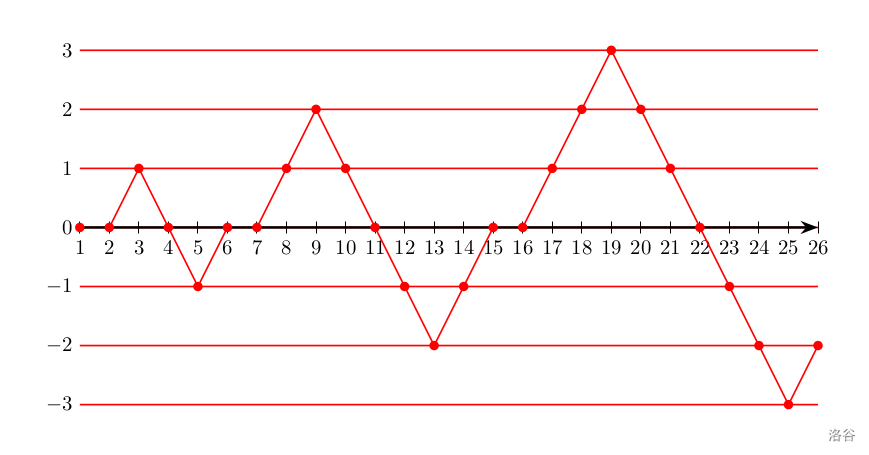
现在梅莉对市场发起了 $q$ 次询问，每次她会给定一个 $k$，希望求出 $a_k$ 是多少。

输入格式

第一行有一个正整数 $q$，表示询问次数。
接下来 $q$ 行，每行一个正整数 $k$，描述每次询问。

输出格式

输出共 $q$ 行。对于每次询问，输出对应的结果。

样例 #1

样例输入 #1

样例输出 #1

提示

对于所有数据，$1 \leq q \leq 10^5$，$1 \leq k \leq 4\times 10^{18}$。

我的答案

#include <iostream>
#include<stdlib.h>
#include<stdio.h>
#include <vector>
using namespace std;
int ranger(long long left,long long right,long long target,long long number){
    if( target >= left && target <= right){
        int num = target - left;
        switch (num / number) {
            case 0: return num-left;
            case 1: return 2*number-num;
            case 2: return -(num-2*number);
            case 3: return -(right-target);
            case 4: return 0;
            default: return -1;
            }
        }
    number++;
    return ranger(right+1,right+1+4*number,target,number);
    }

int main(){
    long n;
    cin >> n;
    vector<long long> input(n);
    for(int i = 0;i < n;i ++){
        cin >> input[i];
    }
    for(int i = 0;i < n;i ++){
        if(input[i] == 1||input[i] == 0){
            cout << 0 << endl;
            continue;
        }
        else
            cout << ranger(2, 6, input[i], 1) << endl;
    }

	return 0;
}

G-二人的花纹纸游戏

题目背景

如果遇到提交失败，请多次刷新，多次提交，会有成功几率

梅莉买到了一张特殊的带有花纹的纸。整张纸的图案可以视为，由一个较小的图案，沿着横向与纵向无限循环而成。同时，这个基本图案部分透明，部分不透明。

于是，如果将这张纸覆盖在书本上，那么一些字可以被看见，另一些字看不见。

莲子突发奇想：假使她制作一张很大很大的数表，将花纹纸覆盖在上面，那么就会有很多数字被遮挡。那些没有被遮挡的数字的和是多少呢？

题目描述

事实上，二人的问题可以转化成如下描述：给定一个 $n$ 行 $m$ 列的普通矩阵 $A$，以及一个 $r$ 行 $c$ 列的 $01$ 矩阵 $B$。$B$ 中为 $1$ 的格子是黑色，不透明；为 $0$ 的格子是透明的。

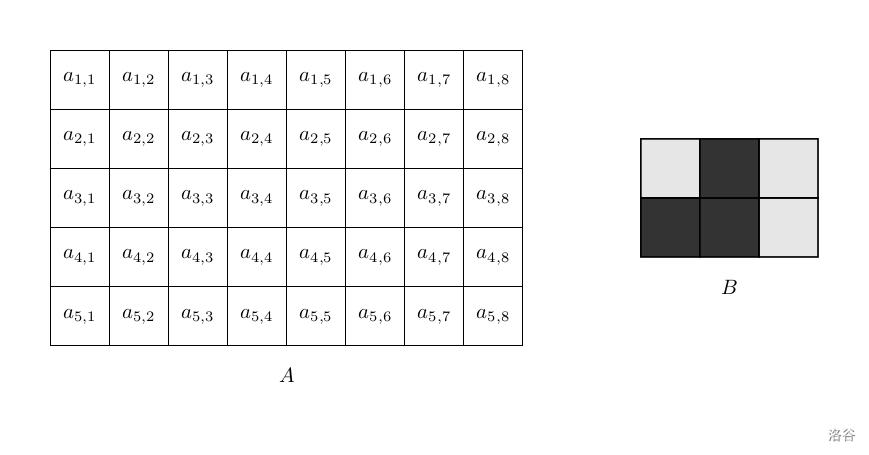
使用 $B$ 矩阵，循环生成一个无穷大的矩阵 $M$：

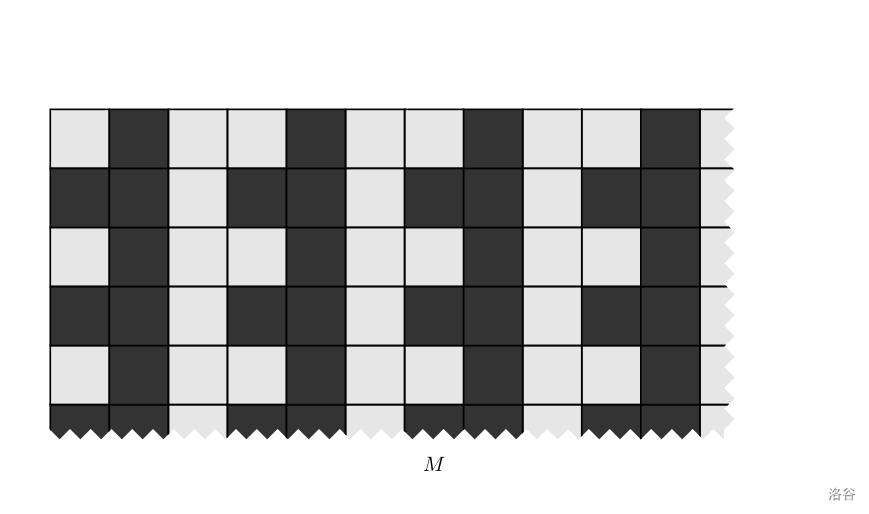
现在有 $q$ 次询问。每次将 $M$ 矩阵左上角和 $(x_1,y_1)$ 对齐，此时此时会有一些 $A$ 中的元素被遮挡，另一些元素可以被看见。

求出此时，$A$ 当中以 $(x_1,y_1)$ 作为左上角，$(x_2,y_2)$ 作为右下角的子矩阵中，可以被看见的元素之和。结果对 $998{,}244{,}353$ 取模。

在上面的例子里，$(x_1,y_1)=(2,3)$，$(x_2,y_2)=(4,7)$。可以被看见的元素之和为 $a_{2,3}+a_{2,5}+a_{2,6}+a_{3,5}+a_{4,3}+a_{4,5}+a_{4,6}$。

形式化题面

给定一个 $n$ 行 $m$ 列的普通矩阵 $A$，以及一个 $r$ 行 $c$ 列的 $01$ 矩阵 $B$。使用 $B$ 矩阵，生成一个无穷大的矩阵 $M$：

$$M=
\begin{pmatrix}
B & B & B &\cdots \
B & B & B &\cdots \
B & B & B &\cdots \
\vdots &\vdots &\vdots &
\end{pmatrix}
=\begin{pmatrix}
b_{1,1} & b_{1,2} & \cdots & b_{1,c} & b_{1,1} & b_{1,2} & \cdots & b_{1,c} & b_{1,1} & \cdots \
b_{2,1} & b_{2,2} & \cdots & b_{2,c} & b_{2,1} & b_{2,2} & \cdots & b_{2,c} & b_{2,1} & \cdots \
\vdots & \vdots & & \vdots & \vdots & \vdots & & \vdots & \vdots & \
b_{r,1} & b_{r,2} & \cdots & b_{r,c} & b_{r,1} & b_{r,2} & \cdots & b_{r,c} & b_{r,1} & \cdots \
b_{1,1} & b_{1,2} & \cdots & b_{1,c} & b_{1,1} & b_{1,2} & \cdots & b_{1,c} & b_{1,1} & \cdots \
b_{2,1} & b_{2,2} & \cdots & b_{2,c} & b_{2,1} & b_{2,2} & \cdots & b_{2,c} & b_{2,1} & \cdots \
\vdots & \vdots & & \vdots & \vdots & \vdots & & \vdots & \vdots & \
b_{r,1} & b_{r,2} & \cdots & b_{r,c} & b_{r,1} & b_{r,2} & \cdots & b_{r,c} & b_{r,1} & \cdots \
\vdots & \vdots & & \vdots & \vdots & \vdots & & \vdots & \vdots & \
\end{pmatrix}$$

现在有 $q$ 次询问，每次给出一个子矩阵的左上角坐标 $(x_1,y_1)$ 和右下角坐标 $(x_2,y_2)$，你需要求出：

$$S=\left(\sum_{i=x_1}^{x_2}\sum_{j=y_1}^{y_2}a_{i,j}\times [M_{i-x_1+1,j-y_1+1}=0] \right)\bmod 998{,}244{,}353$$

其中 $[P]$ 表示艾弗森括号。若 $P$ 为真，则 $[P]=1$，否则 $[P]=0$。

输入格式

第一行有两个正整数 $n,m$，描述矩阵 $A$ 的大小。
接下来 $n$ 行 $m$ 列，每行一个非负整数，描述 $A$ 中的元素 $a_{i,j}$。
下一行有两个正整数 $r,c$，描述矩阵 $B$ 的大小。
接下来 $r$ 行 $c$ 列，每行一个非负整数，描述 $B$ 中的元素 $b_{i,j}$。
下一行有一个正整数 $q$，表示询问的次数。
接下来 $q$ 行，每行有四个正整数 $x_1,y_1,x_2,y_2$，描述一组询问。保证 $x_1\le x_2$，$y_1\le y_2$。

输出格式

输出共 $q$ 行。每行输出该次询问的答案。

样例 #1

样例输入 #1

样例输出 #1

1
2

40
20

样例 #2

样例输入 #2

样例输出 #2

1
2
3

14
17
0

提示

样例 1 解释

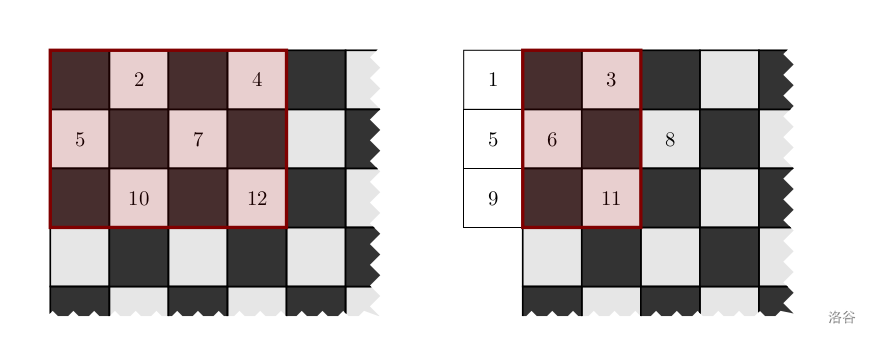
对于第一次询问，结果为 $2+4+5+7+10+12=40$；
对于第二次询问，结果为 $3+6+11=20$。

数据范围及约定

对于全部数据，保证 $1\le n,m\le 10^3$，$1\le q\le 10^4$，$1\le r,c\le 50$，$0\le a_{i,j}<998{,}244{,}353$，$b_{i,j}\in{0,1}$。

我的答案

/*
 * 
 * Copyright (C) 2022 jhsy
 *
 * creat date 2022-11-26 16:51
 *
 */

#include<iostream>
#include <vector>

using namespace std;
int main(){
    int n,m;
    cin >> n >> m;
    vector<vector<int> > inputm(n,vector<int>(4));
    for(int i = 0;i<n;i++){
        for(int j = 0;i<m;j++){
            cin >> inputm[i][j];
        }
    }
    cin >> n >> m;
    vector<vector<int> > inputp(n ,vector<int>(m));
    for(int i = 0;i<n;i++){
        for(int j = 0;i<m;j++){
            cin >> inputp[i][j];
        }
    }
    int ansroud;
    cin >> ansroud;
    vector<vector<int> > position(ansroud,vector<int>(4));
    for(int i = 0;i < ansroud;i++){
        for(int j = 0;j < 4;j++){
            cin >> position[i][j];
        }
    }
    // input done
    //
    for (int i = 0; i < ansroud; i++) {
        int ans = 0;
        for (int y = position[i][1]; y < position[i][3]; y++) {
            int currenty = y - position[i][1];
            for (int x = position[i][0]; x < position[i][2]; x++){
                int currentx = x - position[i][0];
                if(inputp[currenty % n][currentx % m] == 0) ans += inputm[y][x]; 
            }
        }
        cout << ans % 998244353 << endl;
    }
	return 0;
}

H-二人的世界

题目背景

如果遇到提交失败，请多次刷新，多次提交，会有成功几率

莲子设计了一个三维立体空间软件。这个软件可以模拟真实的物理引擎，包括实体方块和水流方块。然而，同时计算大量水流会对软件造成不小的负荷。

于是，莲子希望找到这样一种算法，快速计算这些水流模拟后的结果。

题目描述

莲子设计的水流模型是这样的：

考虑一个三维空间。这个空间内有 $n$ 个正方体。我们使用坐标 $(x_i,y_i,h_i)$ 描述每个正方体的位置。这些正方体，可以被称作实体方块。

现在将会在这张图中模拟一种水流机制。具体而言，我们会定义水方块。水方块会有一个强度 $s$，范围是 $[1,k]$。

运行逻辑

假定 $(x,y,h)$ 处有强度为 $s$ 的水方块，且 $(x,y,h-1)$ 位置没有实体方块，那么下一时刻 $(x,y,h-1)$ 位置会生成强度为 $k$ 的水方块。注意：无论此时 $s$ 的值是多少，在 $(x,y,h-1)$ 位置生成的水方块的强度都是 $k$。
假定 $(x,y,h)$ 处有强度为 $s$ 的水方块，且 $s>1$，且 $(x,y,h-1)$ 位置有实体方块，那么会进行扩散操作。
如果下一时刻，某个位置 $(x,y,h)$ 同时有多个水方块会生成，那么最终生成的水方块的强度，是这些可能生成的水方块里，最大的强度。

扩散操作

考虑到扩散操作比较抽象，建议结合图示理解。

对于水方块 $(x,y,h)$，它会在高度 $h$ 的平面上进行寻路。为了考虑这个过程，我们考虑这个高度为 $h$ 的平面：

如果空间里 $(x,y,h)$ 位置有实体方块存在，那么平面上 $(x,y)$ 处不可经过。否则，如果没有实体方块，那么 $(x,y)$ 处可以经过。
在 $(x,y)$ 可以经过的情况下，如果空间里 $(x,y,h-1)$ 位置没有实体方块存在，那么平面上 $(x,y)$ 位置称为目标位置。目标位置可以不止一个。

根据扩散的前提条件，可知平面上 $(x,y)$ 位置可以经过，但不是目标位置。

从平面上 $(x,y)$ 处出发，进行路径的搜索。每次在 $(a,b)$ 位置会向 $(a+1,b),(a-1,b),(a,b+1),(a,b-1)$ 位置扩展。搜索过程会找到距离 $(x,y)$ 位置最近的，且距离不超过 $s-1$ 的所有目标位置，或者找不到这样的目标位置。

如果存在这样的目标位置，那么在到达目标位置的最短路的方向上，下一时刻会生成一个强度为 $s-1$ 的水方块。
如果不存在这样的目标位置，那么下一时刻，会向 $(x+1,y),(x-1,y),(x,y+1),(x,y-1)$ 位置都生成强度为 $s-1$ 的水方块（如果这个位置可以到达的话）。

请结合图示理解扩散过程。

如图所示。$S$ 处是平面上该水方块所在的位置。白色的方块是目标位置，打 $\times$ 的方块是不可经过的位置。我们计算出 $S$ 到达最近的目标位置的最小值 $d_{\min}=5$，图中标出来的红色路径就是三条可能的最短路。

如果 $s>5$，那么下一时刻，在蓝色箭头处会有强度为 $s-1$ 的水方块生成。否则，若 $5\ge s>1$，那么下一时刻除了蓝色箭头外，灰色路径对应的方向也会生成强度为 $s-1$ 的水方块。

为了检验水流模型的合理性以及其运行效率，莲子提出了这个问题：在 $(x_0,y_0,10^9+1)$ 处，有一个强度为 $k$ 的水方块。询问：在经过充分长的时间后（比如经过了 $10^{9961^{9961}}$ 时刻），有多少个点对 $(a,b)$，满足在 $(a,b,-1)$ 位置，会有水方块生成过。

输入格式

第一行有两个正整数 $n,k$ 和两个整数 $x_0,y_0$，描述实体方块的个数、水方块最大强度，以及初始水方块的位置。
接下来 $n$ 行，每行三个整数 $x_i,y_i,h_i$，描述每个实体方块的位置。保证不存在两个位置完全相同的实体方块。

输出格式

输出共一行一个整数，表示有多少个点对 $(a,b)$，使得充分长时间后 $(a,b,-1)$ 位置有水方块生成过。

样例 #1

样例输入 #1

样例输出 #1

样例 #2

样例输入 #2

样例输出 #2

提示

样例 1 解释

（图片实在太难画啦，将就一下吧。）为了防止方块阻挡导致看不见，方块全部换成了透明的。

初始状态下一根水流柱从高空落下，落在了方块 $(3,4,2)$ 上，进行了扩散。水方块的坐标为 $(3,4,3)$，强度为 $3$。

如图 $3$，根据寻路机制，它会在 $(3,5,3)$ 和 $(4,4,3)$ 上生成强度为 $2$ 的水方块。
如图 $4$，生成的两个支流下方都没有方块，于是在 $(3,5,2)$ 和 $(4,4,2)$ 上生成强度为 $3$ 的水方块。
如图 $5$，水方块 $(3,5,2)$ 下方依旧没有实体方块，于是在 $(3,5,1)$ 生成了强度为 $3$ 的水方块，一直流到 $(3,5,-1)$；水方块 $(4,4,2)$ 下方有实体方块，于是在 $(4,3,2)$ 生成了强度为 $2$ 的水方块。

下面只关心水方块 $(4,3,2)$。它下面有实体方块 $(4,3,1)$，于是它向两边扩散，生成强度均为 $1$ 的两个水方块。这两个方块下面都不再有实体方块，于是一直往下流到 $(4,2,-1)$ 和 $(5,3,-1)$。

因此，最终一共会有三个位置 $(3,5,-1)$、$(4,2,-1)$、$(5,3,-1)$ 有水方块经过。

数据范围及约定

对于所有数据，$1\le n\le 10^5$，$1\le k\le 10^9$，$0\le |x_i|,|y_i|\le 10^9$，$0\le h_i\le 10^9$。