背包问题

  • 01背包问题: 每件物品最多只用一次

  • 完全背包问题: 每件物品有无限个

  • 多重背包问题:

  • 分组背包问题:

01背包问题

01背包模型

有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。

第 i 件物品的体积是 vi，价值是 wi。

求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。
输出最大价值。

首先我们要解决一个问题, 状态表示 和 状态转移

状态表示我们可以用一个数组表示, f[n][m]

  • n表示0 - n个物品选择
  • m表示当前容积

状态转移 第i个物品放入背包和不放入背包的最大值

简单版代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#include<iostream>
using namespace std;

const int N = 1010;
int v[N], w[N];
int f[N][N];
int n, m;

int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i++)
        cin >> v[i] >> w[i];
    
    for(int i = 1; i <=n ; i++)
        for(int j = 0; j <= m; j++)
        {
            f[i][j] = f[i - 1][j];		// 表示第i个物品不放入背包时的价值
          
          	// 如果当前容量大于i的容量, 取放入i和不放i的最大值
            if(j >= v[i]) f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);
          	// 这里的f[i - 1][j - v[i]],表示的是不放入i时候, 体积减去i的体积的最大值, 再加上i的价值
        }
        
    cout << f[n][m];
    
    return 0;
}

优化后的代码

可行性：二维状态转移方程针对第i个物品做规划的时候，所有数据只依赖于第i-1个物品规划的过程，所以可以使用一维滚动数组；

逆序更新：因为j-v[i]小于等于j，所以如果j从0开始规划，那么在更新“选取物品i的选择方案”时，会用本轮（第i个物品规划）的比较小的物品容量j时被更新过的数据，这个数据反映的是本轮针对第i个物品的规划，不是第i-1个物品的规划，所以与原始算法不等价，采取倒序的方式更新，这样可以保留上一轮i-1的信息。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
#include<iostream>
using namespace std;
const int N = 1010;

int n,m;
int v[N], w[N];
int f[N];

int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i++) cin >> v[i] >> w[i];
    
    for(int i = 1; i <= n; i++)
        for(int j = m; j >= v[i]; j--)
          	// 因为优化之前我没要用f[i - 1][j] 来更新 f[i][j] ,我们只需要用到f[i - 1]这一层数据
          	// 所以对于所有的f[i - 1] 直接用f[i] 去替代, 同样因为在更新容量的过程中, 大数据会使用小数据的结果]
          	// 所以不能从小到大遍历, 要从大到小遍历所有容量
            f[j] = max(f[j], f[j - v[i]] + w[i]);

    cout << f[m];
    
    return 0;
}

完全背包问题

模型

有 N 种物品和一个容量是 V 的背包，每种物品都有无限件可用。

第 i 种物品的体积是 vi，价值是 wi。

求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。
输出最大价值。

状态转移和状态表示同01背包问题类似.

我们要解决的问题是, 这个模型要考虑i个物品放入, 而不是0个或者1个

状态转移方程: f[i][j] = max(f[i][j], f[i-1][j - k * v[i]] + k * w[i]); 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#include<iostream>
using namespace std;

const int N = 1010;

int v[N], w[N];
int f[N][N];
int n,m;

int main()
{
    cin >> n >> m;
    for(int i = 1 ; i <= n; i++) cin >> v[i] >> w[i];
    
    for(int i = 1; i <= n; i++)
        for(int j = 0; j <= m; j++)
        {
            f[i][j] = f[i - 1][j];	// 可删去, 便于理解保留
            for(int k = 0; k * v[i] <= j; k++)
            		f[i][j] = max(f[i][j], f[i-1][j - k * v[i]] + k * w[i]);		// 状态转移
        }
        
    cout << f[n][m];
    
    return 0;
}

如果数据过大会TLE, 时间复杂度O(n^3);

我们进一步优化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
#include<iostream>
using namespace std;

const int N = 1010;

int v[N], w[N];
int f[N][N];
int n,m;

int main()
{
    cin >> n >> m;
    for(int i = 1 ; i <= n; i++) cin >> v[i] >> w[i];
    
    for(int i = 1; i <= n; i++)
        for(int j = 0; j <= m; j++)
        {
            f[i][j] = f[i - 1][j];		//  不选i的转移方程
            if(j >= v[i])   
              	f[i][j] = max(f[i][j], f[i][j - v[i]] + w[i]);
          			//  选择i的转移方程
        }
        
    cout << f[n][m];
    
    return 0;
}

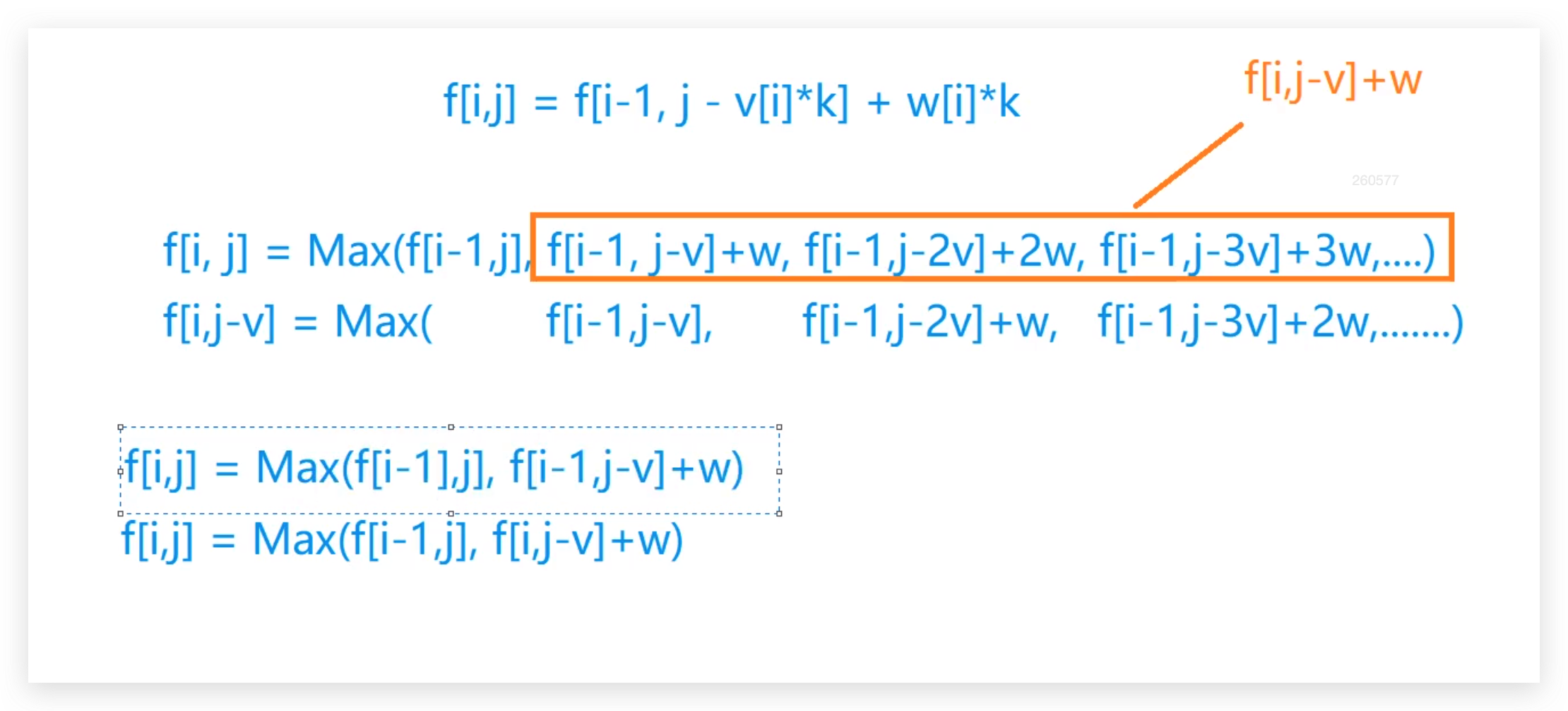
最大的不同主要是体现在选择i时的转移方程,

f[i][j] = max(f[i][j], f[i][j - v[i]] + w[i]);

第一次迭代的意义, f[i][j] = f[i - 1][j]

之后的每一次迭代, f[i][j] = f[i][j - v] + w[i]

表示的意义为 从 1 - i 个物品, 体积逐渐增大, 价值的最大值. 只要容量大于i的体积, 就取i加入前后的最大值

image-20230201124004182

优化为一维数组

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#include<iostream>
using namespace std;

const int N = 1010;

int v[N], w[N];
int f[N];
int n,m;

int main()
{
    cin >> n >> m;
    for(int i = 1 ; i <= n; i++) cin >> v[i] >> w[i];
    
    for(int i = 1; i <= n; i++)
        for( int j = v[i]; j <=m ; j++)
          	//  容量依次增加迭代, 需要向后迭代改变j增大时的数据.
            f[j] = max(f[j], f[j - v[i]] + w[i]);
        
    cout << f[m];
    
    return 0;
}

优化方法同理01背包问题

多重背包问题

模型

有 N种物品和一个容量是 V 的背包。

第 i 种物品最多有 s[i] 件，每件体积是 v[i]，价值是 w[i]。

求解将哪些物品装入背包，可使物品体积总和不超过背包容量，且价值总和最大。
输出最大价值。

我们可以理解为多重背包问题就是在完全背包问题的基础上加了一个物品数量的限制, 即 k <= s[i]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#include<iostream>
using namespace std;

const int N = 110;
int v[N], w[N], s[N];
int n, m;
int f[N][N];

int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i++) cin >> v[i] >> w[i] >> s[i];
    
    for(int i = 1; i <= n; i++)
        for(int j = 0; j <= m ; j++)
            for(int k = 0; k <= s[i] && k * v[i] <= j; k++)
              	// 增加对k的限制
                f[i][j] = max(f[i][j], f[i - 1][j - v[i] * k] + k * w[i]);
    
    cout << f[n][m];
    
    return 0;
}

问题规模比较大时, 时间复杂度比较高会TLE, 所以我们必须进行优化.

我们可以采用二进制优化

  • 将s拆分为n个 2, 4, 8, 16, … c
  • 任意组合即可累计为s内的任意值
  • 最后分解成01背包问题
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
#include<iostream>
using namespace std;
// N的取值等于n 的最大值乘以log s
const int N = 1010 * 12 , V = 2010;
int v[N], w[N], s[N];
int f[N];
int n, m, cnt;

int main()
{
    cin >> n >> m;

    while(n--)
    {
        int a, b, c;
        cin >> a >> b >> c;
        int k = 1;
        while(k <= c)
        {
            cnt++;
            v[cnt] = a * k;
            w[cnt] = b * k;
            c -= k;
            k *= 2;
        }
        if(c > 0)
        {
            cnt++;
            v[cnt] = a * c;
            w[cnt] = b * c;
        }
    }
    
    for(int i = 1; i <= cnt; i++)
        for(int j = m; j >= v[i]; j--)
            f[j] = max(f[j], f[j - v[i]] + w[i]);
            
    cout << f[m];
    return 0;
}

分组背包问题

模型

有 N组物品和一个容量是 V的背包。
每组物品有若干个，同一组内的物品最多只能选一个。
每件物品的体积是 vij，价值是 wij，其中 i是组号，j是组内编号。

求解将哪些物品装入背包，可使物品总体积不超过背包容量，且总价值最大。

输出最大价值。

我们可以看做是一个01背包问题和完全背包问题的组合体

每次在放入一个物品的时候需要遍历一遍每一组内所有的物品,选择其最大值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#include<iostream>
#include<algorithm>
using namespace std;

const int N = 110;

int v[N][N], w[N][N], s[N];
int f[N];
int n, m;

int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i++)
    {
        cin >> s[i];
        for(int j = 0; j < s[i]; j++)
        {
            cin >> v[i][j] >> w[i][j];
        }
    }
    
    for(int i = 1; i <= n; i++)
        for(int j = m; j > 0; j--)
            for(int k = 0; k < s[i]; k++)
              	// 每组内的所有物品都遍历一遍, 因为不知道最小体积是多少,所以我们只能遍历到j = 0再结束
                if(v[i][k] <= j) f[j] = max(f[j], f[j - v[i][k]] + w[i][k]);
                
    cout << f[m];
    return 0;
}

状态转移时的更新问题

我们发现如果需要滚动数组来更新数据的话, 遍历容量的时候要从大到小遍历, 而需要用到本层数据的话则需要从小到大排序.

j较大时,需要用较小的数据来更新. 所以根据问题我们要解决是否要覆盖当前层的数据.