Intro

动态规划算法（Dynamic Programming，简称 DP）

动态规划是一种常见的「算法设计技巧」

动态规划遵循一套固定的流程：

递归的暴力解法 -> 记录数据的递归解法 -> 非递归的动态规划解法。

是常用的一种空间换时间的算法。

我觉得本质是自下向上的递归。

引例

斐波那契数列

我们定义斐波那契数列为：

1
2
3
4
5
6
7
1
1
2
3
5
8
13

每一项为前两项之和，第一项和第二项为1.

我们可以根据以上定义，写一个输出第n项的递归程序

1
2
3
4
int fiber(int n){
  if (n == 1 || n == 2) return 1;
  return fiber(n - 1) + biber(n - 2);
}

想要计算原问题 f(20)。

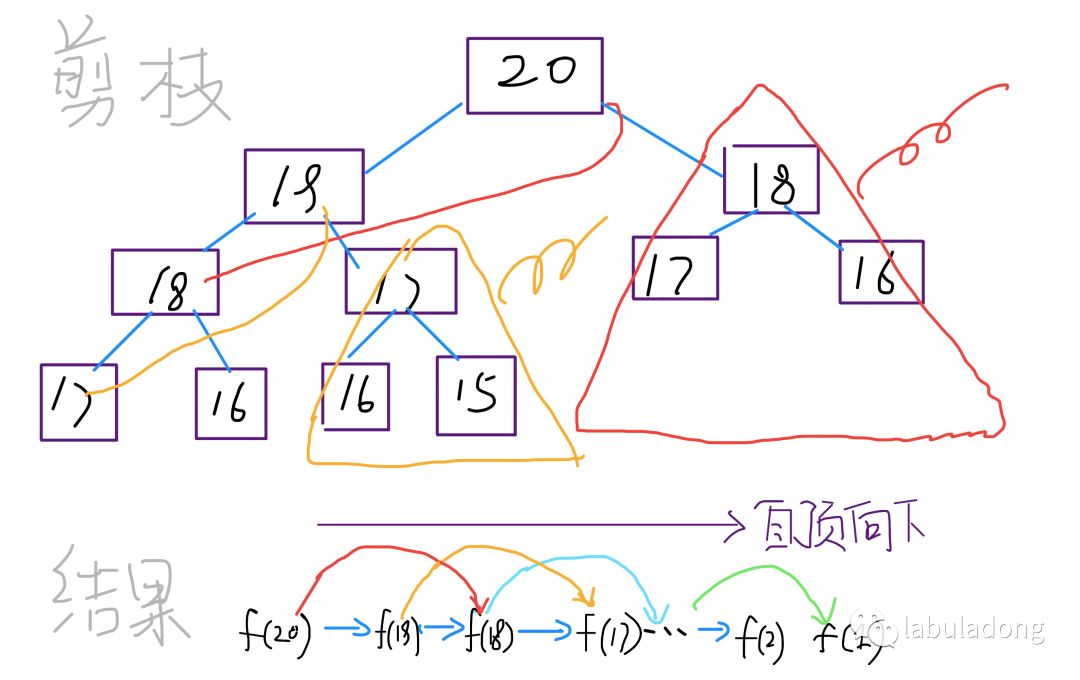
我就得先计算出子问题 f(19) 和 f(18)，然后要计算 f(19)，我就要先算出子问题 f(18) 和 f(17)，以此类推。最后遇到 f(1) 或者 f(2) 的时候，结果已知，就能直接返回结果，递归树不再向下生长了。

时间复杂度计算

子问题个数 乘以 解决一个子问题需要的时间。

  • 子问题个数：递归树中节点的总数。显然二叉树节点总数为指数级别，所以子问题个数为 O(2^n)

  • 子问题时间复杂度：在本算法中，没有循环，只有 f(n - 1) + f(n - 2) 一个加法操作，时间为 O(1)。

    这个算法的时间复杂度为 O(2^n)，指数级别

缺陷

算法中存在大量重复计算，造成时间浪费。f(n-2)和f(n-1)重复出现，每出现一次就需要重复计算值。

*重叠子问题

既然f(n-2)和f(n-1)重复出现，我们可不可以所有重复出现的数值用一个备忘录记录下来，每次只需要直接拿出来用即可。

这就是动态规划问题的第一个性质：重叠子问题。

改进算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int fib(int N) {
    if (N < 1) return 0;
    // 备忘录全初始化为 0
    vector<int> memo(N + 1, 0);
    // 初始化最简情况
    memo[1] = memo[2] = 1;
    return helper(memo, N);
}

int helper(vector<int>& memo, int n) {
    // 未被计算过
    if (n > 0 && memo[n] == 0) 
        memo[n] = helper(memo, n - 1) + helper(memo, n - 2);
    return memo[n];
}

带「备忘录」的递归算法，把一棵存在巨量冗余的递归树通过「剪枝」，改造成了一幅不存在冗余的递归图，极大减少了子问题（即递归图中节点）的个数。

Image

时间复杂度计算

  • 子问题个数：即图中节点的总数，由于本算法不存在冗余计算，子问题就是 f(1), f(2), f(3) … f(20)，数量和输入规模 n = 20 成正比，所以子问题个数为 O(n)。
  • 解决一个子问题的时间，同上，没有什么循环，时间为 O(1)。

改进后的代码时间复杂度为O(n).

总结

带备忘录的递归解法的效率已经和动态规划类似。实际上，这种解法和动态规划的思想已经差不多了，只不过这种方法叫做「自顶向下」，动态规划叫做「自底向上」。

  • 自顶向下：递归树从上向下延伸，将一个规模较大的问题向下逐渐分解成一个小问题，逐层返回答案
  • 自底向上：反过来，我们直接从最小的问题，逐步向上推，得到我们想要的大规模问题的答案。

这就是动态规划的思路，这也是为什么动态规划一般都脱离了递归，而是由循环迭代完成计算。

动态规划

有了上一步「备忘录」的启发，我们可以把这个「备忘录」独立出来成为一张表，就叫做 DP table 吧，在这张表上完成「自底向上」的推算。

1
2
3
4
5
6
7
int fib(int N) {
    vector<int> dp(N, 0);
    dp[0] = dp[1] = 1;
    for (int i = 3; i < N; i++)
        dp[i] = dp[i - 1] + dp[i - 2];
    return dp[N-1];
}

*状态转移方程

若f(n)为一个状态n，则这个状态n就是由状态n-1加上状态n-2相加转移而来。

img

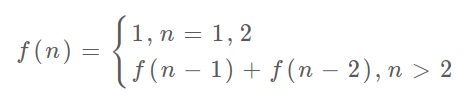
上面的几种解法中的所有操作，例如 return f(n - 1) + f(n - 2)，dp[i] = dp[i - 1] + dp[i - 2]，以及对备忘录或 DP table 的初始化操作，都是围绕这个方程式的不同表现形式。可见列出状态转移方程的重要性，它是解决问题的核心。很容易发现，其实状态转移方程直接代表着暴力解法。

动态规划问题最困难的就是写出状态转移方程

关于斐波那契数列最后一个优化。即并不需要储存从1到n之间所有的结果。我们只需要储存前两个结果并依次向后迭代即可。

1
2
3
4
5
6
7
8
9
10
int fib(int n) {
    if (n < 2) return n;
    int prev = 0, curr = 1;
    for (int i = 0; i < n - 1; i++) {
        int sum = prev + curr;
        prev = curr;
        curr = sum;
    }
    return curr;
}

这一般是动态规划问题的最后一步优化，如果我们发现每次状态转移只需要 DP table 中的一部分，那么可以尝试缩小 DP table 的大小，只记录必要的数据，从而降低空间复杂度。

凑零钱问题

题目：给你 k 种面值的硬币，面值分别为 c1, c2 … ck，再给一个总金额 n，问你最少需要几枚硬币凑出这个金额，如果不可能凑出，则回答 -1 。

我提交的答案

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
int coinChange(vector<int>& coins, int amount) {
        if (amount ==0 ) {
        return 0;
        }
        int ans = 0;
        sort(coins.begin(),coins.end());
        for(int j = coins.size() - 1; j >= 0 ; j--){
            if(amount >= coins[j]){
                int i = amount / coins[j];
                amount -= coins[j] * i;
                ans += i;
            }
        }
        if (amount == 0) {
            return ans;
        }
        else return -1;
    }

有点像贪心了，每次都取最优质值。然后再将剩下的数额再进行计算。如果出现最大数值最大情况凑不整。算法则会失败。

1
2
[186,419,83,408]
6249

如上结果算法失败。

递归

用递归的方法去做这道题。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int dp(vector<int> coins,int amount){
    if(amount == 0) return 0;
    if(amount < 0 ) return -1;
    int res = INT_MAX;
    for (int i = 0;i < coins.size();i++) {
        int subproblem = dp(coins,amount-coins[i]);
        if (subproblem == -1) {
            continue;
        }
        res = min(res,subproblem+1);
    }
    return res == INT_MAX ? -1:res;
}

int coinChange(vector<int>& coins, int amount) {
    return dp(coins,amount);
}

如果数额为0则直接返回0，如果小于0说明当前数值凑不齐。

画出程序递归树，由于每个节点都有n个分支，且数值越大问题规模越大，时间复杂度为O(n^j);

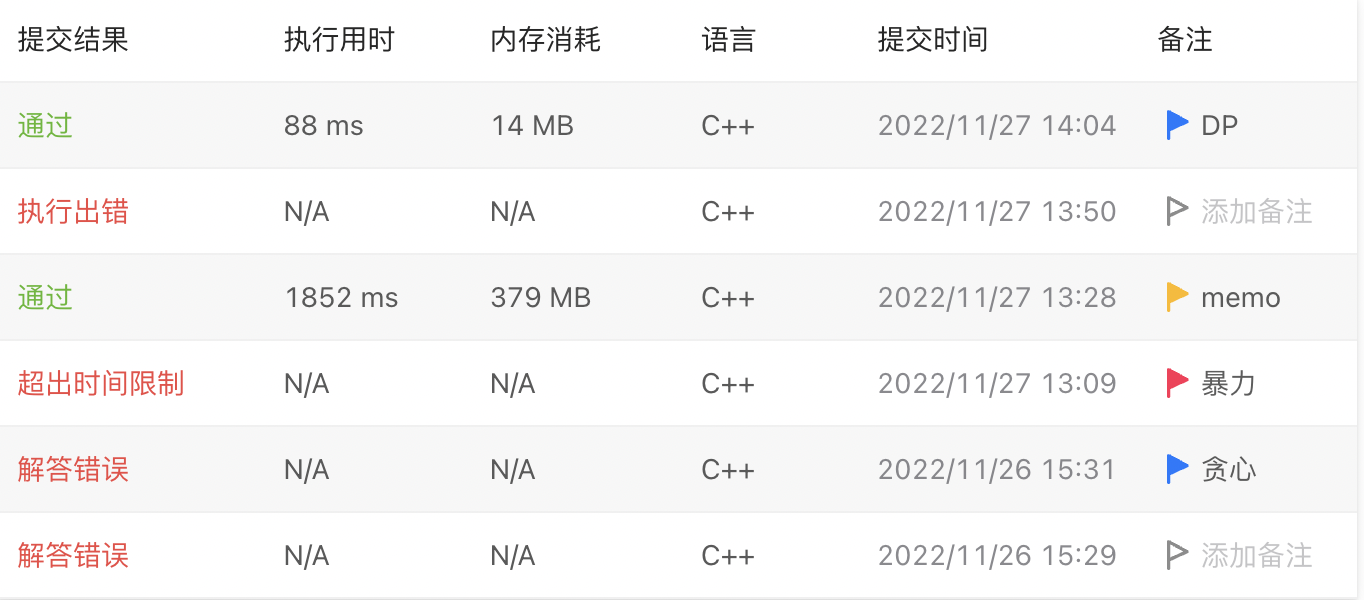
执行时间超出时间限制

使用memo数组记录数据

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
    int dp(vector<int> coins,int amount,vector<int> &memo){
        if(amount == 0) return 0;
        if(amount < 0 ) return -1;
        int res = INT_MAX;
      // 如果memo没有被计算过，则计算memo的值，如果被计算过直接返回memo的值
        if (memo[amount]== -10) {
            for (int i = 0;i < coins.size();i++) {
                int subproblem = dp(coins,amount-coins[i],memo);
                if (subproblem == -1) {
                    continue;
                }
                res = min(res,subproblem+1);
            }
            memo[amount] = res == INT_MAX ? -1:res;
        }
        return memo[amount];
    }

    int coinChange(vector<int>& coins, int amount) {
        vector<int> memo(amount+1,-10);
// 定义一个不会被使用到的值作为未计算标志
        return dp(coins,amount,memo);
    }

执行时间1852ms

虽然这次能过AC但是 执行时间太久。

自下而上建立memo数组（动态规划）

1
2
3
4
5
6
7
8
9
10
11
12
int coinChange(vector<int>& coins, int amount) {
    vector<int> memo(amount+1,amount+1);
    memo[0] = 0;
    for(int i = 1;i <= amount;i ++){
        for(int j = 0;j<coins.size();j++){
            if (i - coins[j] >= 0){
            memo[i] = min(memo[i], memo[i-coins[j]] + 1);
            }
        }
    }
    return memo[amount]>amount?-1:memo[amount];
}

自下而上建立memo数组。

首先初始化amount = 0时，返回值为0

以上不同算法的提交记录

https://leetcode.cn/problems/coin-change

image-20221127141257932

解题思路

首先，动态规划问题的一般形式就是求最值。动态规划其实是运筹学的一种最优化方法，只不过在计算机问题上应用比较多，比如说让你求最长递增子序列，最小编辑距离等等。

既然是要求最值，核心问题是什么呢？求解动态规划的核心问题是穷举。因为要求最值，肯定要把所有可行的答案穷举出来，然后在其中找最值呗。

动态规划这么简单，就是穷举就完事了？我看到的动态规划问题都很难啊！

首先，虽然动态规划的核心思想就是穷举求最值，但是问题可以千变万化，穷举所有可行解其实并不是一件容易的事，需要你熟练掌握递归思维，只有列出正确的「状态转移方程」，才能正确地穷举。而且，你需要判断算法问题是否具备「最优子结构」，是否能够通过子问题的最值得到原问题的最值。另外，动态规划问题存在「重叠子问题」，如果暴力穷举的话效率会很低，所以需要你使用「备忘录」或者「DP table」来优化穷举过程，避免不必要的计算。

以上提到的重叠子问题、最优子结构、状态转移方程就是动态规划三要素。具体什么意思等会会举例详解，但是在实际的算法问题中，写出状态转移方程是最困难的，这也就是为什么很多朋友觉得动态规划问题困难的原因，我来提供我总结的一个思维框架，辅助你思考状态转移方程：

明确 base case -> 明确「状态」-> 明确「选择」 -> 定义 dp 数组/函数的含义。

总结

计算机解决问题其实没有任何奇技淫巧，它唯一的解决办法就是穷举，穷举所有可能性。算法设计无非就是先思考“如何穷举”，然后再追求“如何聪明地穷举”。

列出状态转移方程，就是在解决“如何穷举”的问题。之所以说它难，一是因为很多穷举需要递归实现，二是因为有的问题本身的解空间复杂，不那么容易穷举完整。

备忘录、DP table 就是在追求“如何聪明地穷举”。用空间换时间的思路。